No hay duda que las matemáticas nos ayudan a entender el mundo que nos rodea y por ende, a transformarlo, y las ecuaciones no son la excepción.
De hecho, en 2013, el autor Ian Stewart, un matemático y científico británico de renombre, publicó una obra titulada Las 17 ecuaciones que cambiaron el mundo (Ed. Robert Laffont).
Si quieres entender por qué las matemáticas son tan importantes y qué impactos ha tenido cada ecuación matemática, a continuación te presentamos 15 ecuaciones importantes en la historia de la humanidad.
Aunque antes, explicamos brevemente qué es una ecuación y hablamos sobre cuál es la ecuación más difícil del mundo.
Las ecuaciones existen desde hace milenios: los babilonios ya resolvían ecuaciones cuadráticas ¡hace más de 4,000 años!

¿Qué es ecuación en matemáticas?
Imagina que una ecuación es como un juego de equilibrio. Tienes dos lados, separados por un signo de igual (=), y la idea es que ambos lados valgan lo mismo.
Por ejemplo, si de un lado tienes 2 + 3 y del otro 5, la balanza está perfectamente equilibrada porque ambos suman lo mismo. En pocas palabras, una ecuación es una forma de decir que dos cosas distintas representan el mismo valor.
Lo divertido (sí, divertido) de las ecuaciones es que muchas veces aparece una incógnita, generalmente representada con letras como x o y.
Esa incógnita es como un misterio por resolver: ¿qué número hace que la balanza quede en equilibrio? Resolver una ecuación es justo eso: descubrir el valor escondido que mantiene la igualdad.
Así, las ecuaciones se vuelven un reto entre tú y las matemáticas, y al resolverlas, desarrollas tu ingenio y tu lógica.
Aprende más con un curso de geometría diferencial.
¿Cuál es la ecuación más difícil del mundo?
Varias son las ecuaciones más difíciles, por lo que decir cuál es la ecuación más difícil del mundo no es tan sencillo, pues depende de a quién le preguntes.
Para alguien que empieza a aprender matemáticas, una ecuación como 2x + 5 = 15 puede parecer un verdadero reto. Pero en el mundo de las matemáticas avanzadas, hay ecuaciones tan complejas que generaciones enteras de científicos han dedicado sus vidas a tratar de resolverlas.
Un ejemplo famoso son las ecuaciones de Navier-Stokes, que describen cómo se mueve un fluido (como el aire o el agua).
Aunque parecen “simples” en su forma, esconden tanta complejidad que todavía hoy los matemáticos no saben resolverlas completamente, y de hecho, hay un premio de un millón de dólares para quien logre darles una solución general.
Otro caso es la Ecuación de Yang–Mills, también con premio millonario pendiente. Así que, más que hablar de una sola ecuación imposible, podríamos decir que lo más difícil es ese conjunto de problemas abiertos que siguen desafiando a las mentes más brillantes del planeta.
15 ecuaciones importantes en la historia
Si te encantan las matemáticas y sus problemas, seguramente te has preguntado cuáles son las ecuaciones más importantes en la historia. Y es que hay bastantes que han marcado el rumbo de la humanidad, pero aquí seleccionamos las 15 ecuaciones más relevantes:
1. El teorema de Pitágoras
Este teorema es seguramente uno de los más conocidos.
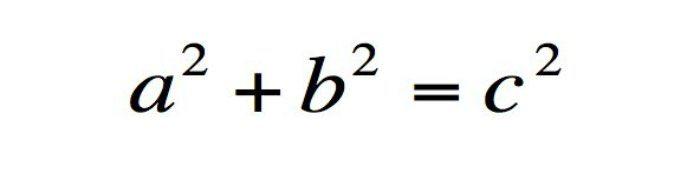
Incluso tras algunos años sin estudiar matemáticas, seguro que el nombre de este teorema todavía se encuentra en algún rincón de tu memoria.
Todo el mundo lo conoce, pero vamos a refrescarte la memoria: en un triángulo rectángulo, el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos.
Este teorema, que data del 530 a.C., es una de las bases de las matemáticas de hoy en día y ha contribuido a la historia de las matematicas de secundaria desde siempre.
Esta fórmula es esencial para entender mejor la geometría; de hecho, esta ecuación ha cambiado nuestra forma de ver la geometría, es decir, de una forma plana. Se dice que pasamos de una geometría euclidiana a una geometría no euclidiana.
A partir de entonces, gracias a Pitágoras y a su famosa ecuación, es fácil calcular longitudes y ángulos y demostrar que un triángulo es rectángulo.
Esta noción se encuentra a menudo en el mundo de la construcción y de la arquitectura.
El signo “=” se inventó en 1557 por el matemático galés Robert Recorde. Lo creó porque estaba cansado de escribir “es igual a” una y otra vez.
¿Necesitas más motivos para aprender matemáticas? Descubre 6 razones de peso para estudiar esta disciplina.
2. El teorema de Tales: ¡la otra fórmula matemática fundamental!
Este es un segundo pilar de las matemáticas del colegio: ¡el famoso teorema de Tales!
¿Sabías que este teorema no es de Tales, sino de Euclides?
Se le atribuyó a Tales por la leyenda de la medida de la pirámide, luego lo veremos. Veamos este teorema que le quita el sueño a más de uno.
Si en un triángulo se traza una línea paralela a cualquiera de sus lados, se obtiene un triángulo que es semejante al triángulo dado"
Del establecimiento de la existencia de una relación de semejanza entre ambos triángulos se deduce la necesaria proporcionalidad entre sus lados. Este corolario es la base de la geometría descriptiva.
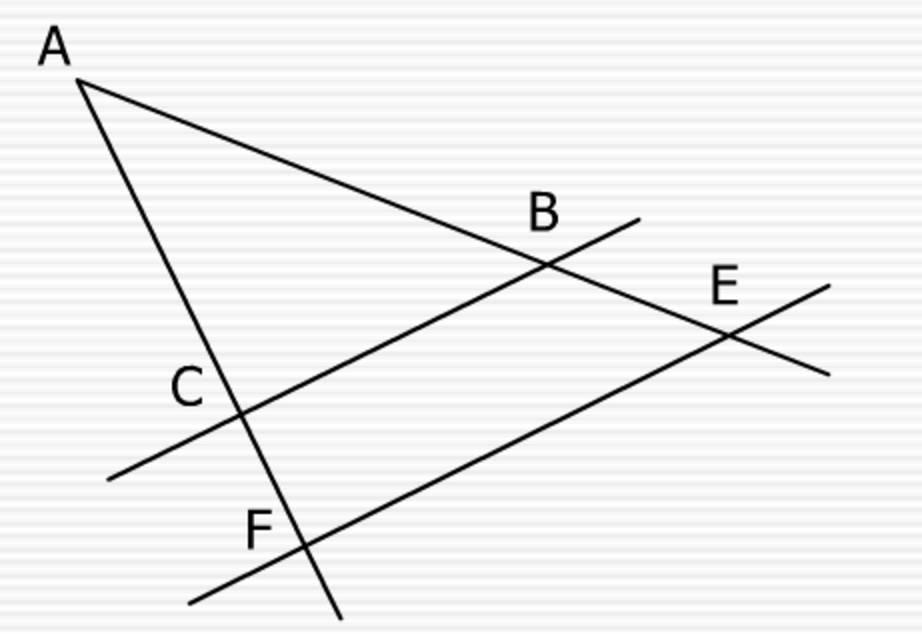
Pero ¿por qué el teorema de Tales revolución las matemáticas? ¿Cómo aporta una solución matemática real a problemas concretos?
En geometría, el teorema de Tales, así como su corolario, pueden utilizarse para demostrar y establecer condiciones de alineamiento o de paralelismo.
La leyenda cuenta que a petición del rey Amasis, Tales fue a Egipto para calcular la altura de las pirámides, y en concreto la de Keops. Colocando un bastón en vertical a mediodía, le dijo al rey: "La relación con respecto a mi sombra es la misma que la de la pirámida con respecto a la suya".
Así, en otros términos, si la longitud del bastón, así como su sombra, son sabidas, es posible, aplicando las mismas proporciones, determinar la altura de las pirámides, tras medir la sombra.
Si quieres clases de matematicas para entrar a la secundaria, explora las clases de matematicas sexto grado.
3. Los logaritmos
Los logaritmos, popularizados por John Napier en 1610, agrupan funciones inversas, opuestas y exponenciales.
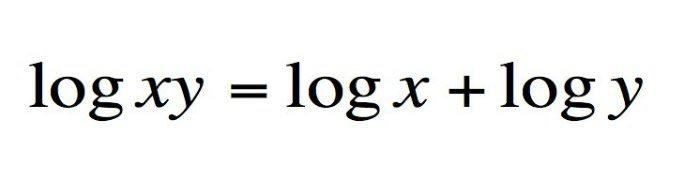
Hasta la llegada del ordenador, el cálculo con logaritmos era la forma más habitual de multiplicar un número grande, lo que permitió calcular de forma más rápida, pero sobre todo hacer grandes avances en los dominios de las matemáticas, la física e incluso de la ingeniería y la astronomía.
Hay tres tipos de logaritmos:
- El logaritmo neperiano es la base fundamental en el análisis matemático
- El logaritmo decimal se utiliza en cálculos matemáticos
- El logaritmo binario se utiliza en la teoría informática y para cálculos aplicados
El logaritmo de un número es el exponente al que hace falta elevar su base para obtener dicho número.
Por ejemplo, en lo que respecta a la base 10, el logaritmo (log) es: Log (1) = 0, log (10) = 1, log (100) = 2.
Aunque no lo parezca, las ecuaciones también inspiran arte, por la espiral logarítmica, que se describe con una ecuación, aparece en conchas marinas, galaxias y hasta en cuadros de artistas renacentistas.
¿Necesitas un curso basico de algebra?
4. La ley de la gravedad
¿Quién no ha oído nunca hablar de la ley de la gravedad de Isaac Newton? Ya sabes, la historia de la manzana que le cayó en la cabeza al erudito mientras miraba la Luna en el cielo. Eso pasó en 1687.
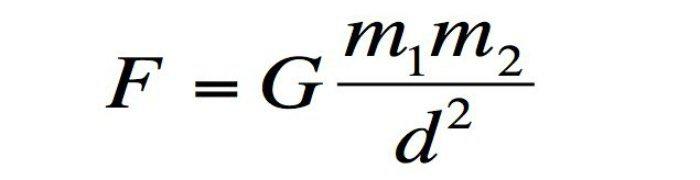
Tras la caída de la manzana, miró de nuevo la Luna y pensó: ¿por qué la Luna no se cae? La respuesta es evidente: la «retiene» una fuerza gravitatoria.
Así fue como nació la célebre fórmula de la ley de la gravedad de Newton: «los astros se atraen de forma proporcional al producto de sus masas e inversamente proporcional al cuadrado de la distancia que los separa».
Doscientos años más tarde, Einstein remplazará la teoría de la gravitación por su teoría de la relatividad.
¿Quieres saber para qué sirven las matemáticas en nuestro día a día?
5. La teoría de la relatividad
Tanto los expertos en las matemáticas y la física como los que solo conocen los fundamentos básicos de las matemáticas, todo el mundo conoce la famosa fórmula E = mc² de Albert Einstein.
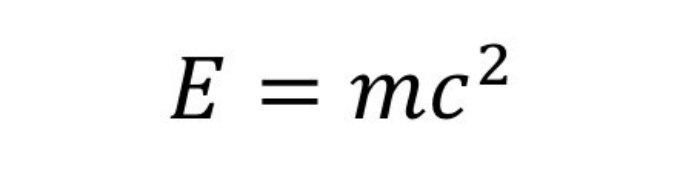
Esta fórmula que ilustra la teoría de la relatividad alteró todos los códigos de la física conocidos hasta entonces.
Actualmente, sigue siendo crucial, ya que muestra que la materia puede convertirse en energía y viceversa.
La relatividad especial, o restringida, aporta la idea de que la velocidad de la luz es una constante universal que no cambia y que el paso del tiempo no es el mismo para las personas que se desplazan a velocidades diferentes.
La relatividad general de Einstein describe la gravedad donde existe un espacio-tiempo curvado y plegado, lo que supuso un cambio fundamental tras la ley de la gravedad de Newton.
Actualmente, todavía es esencial la teoría de la relatividad de Einstein para entender el origen, la estructura y el destino de nuestro Universo.
Si te apasionan los enigmas, los acertijos y las adivinanzas, échale un ojo a Enigmas Matemáticos Difíciles de Resolver.
6. La teoría del caos
Lo que es interesante de la teoría del caos es que ha demostrado que no se puede predecir con determinación lo que va a ocurrir.
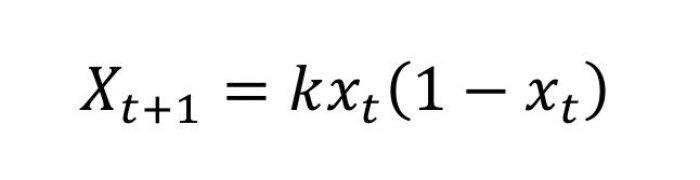
Esta teoría prueba que no existe ningún proceso que se pueda pronosticar.
La teoría de Robert May es muy reciente, ya que data de 1975 y describe un proceso en constante evolución a través del tiempo.
En su fórmula, May quiso explicar que un comportamiento caótico (como la meteorología que conoce muchos cambios climáticos regularmente, incluso ínfimos) puede conducir a otro sistema completamente diferente unos días más tarde.
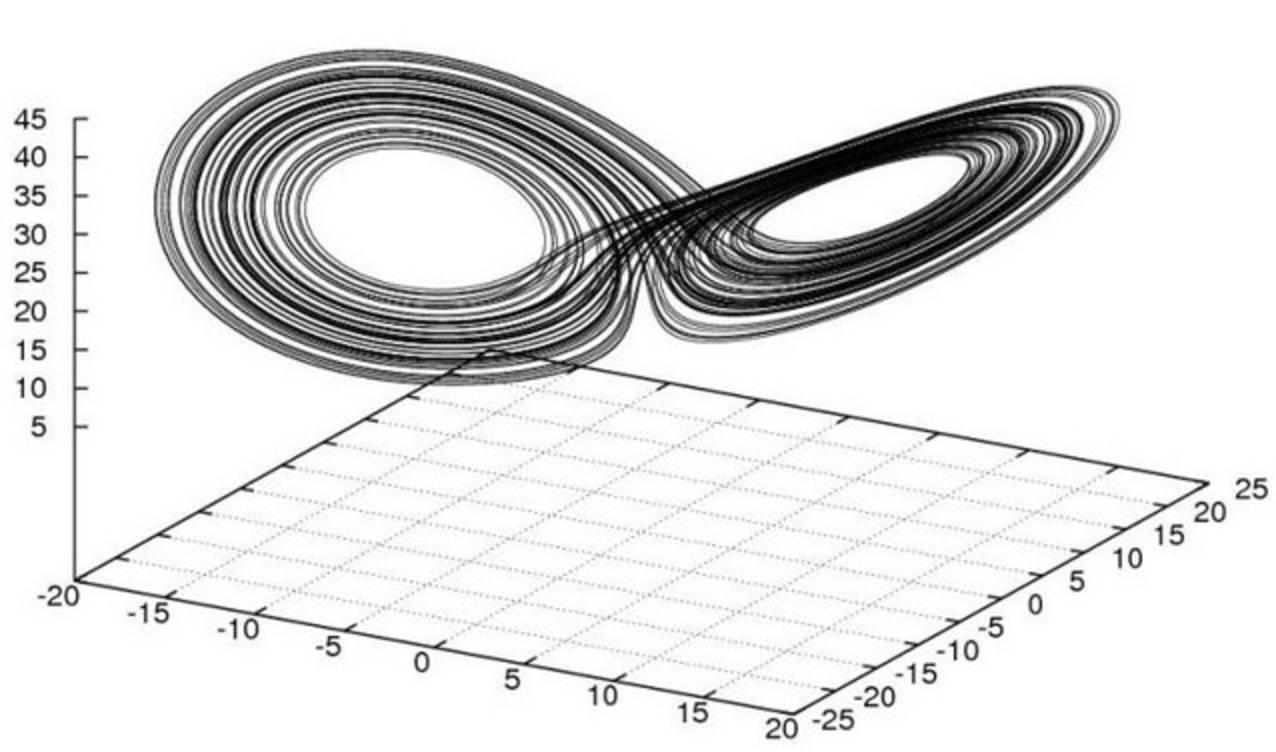
El concepto más conocido es el del «efecto mariposa» que afirma que «el aleteo de las alas de una mariposa puede provocar un tornado al otro lado del mundo».
En otras palabras, las cosas más insignificantes pueden tener un impacto insospechado en nuestro entorno inmediato y menos inmediato.
La multiplicidad de los factores hace que todo acontecimiento sea imprevisible. Recuerda que las ecuaciones son parte fundamental de las clases de algebra.
7. El cálculo infinitesimal
A medio camino entre el álgebra y la geometría, el cálculo infinitesimal es una rama de las matemáticas. El cálculo infinitesimal se centra en las integrales, las series o sucesiones infinitas, las funciones, tratando sus derivadas y sus límites.
Para resumirlo en una sola idea, hablaríamos de estudio de variaciones. Encontramos numerosas aplicaciones concretas en la mecánica, la física o la economía.
En efecto, el estudio de variaciones permite estudiar la evolución de una empresa teniendo en cuenta muchos datos diversos para predecir o dar una idea de su salud financiera en años futuros.
8. La identidad de Euler
La identidad de Euler está considerada como la más bella de las ecuaciones, ya que pone en escena una combinación improbable de cinco constantes matemáticas.
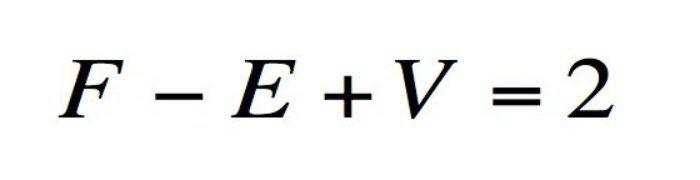
¿Por qué es tan admirada esta ecuación? Porque utiliza tres de las operaciones fundamentales de la aritmética: la suma, la multiplicación y el exponente.
Las 5 constantes representadas con el «0», que es el elemento neutro de la suma:
- el «1», que es el elemento neutro de la multiplicación;
- el número pi; la «e», que es la base de los logaritmos (y que aparece a menudo en análisis y cálculos diferenciales)
- la «i», que es la unidad imaginaria, a partir del cual se construye el conjunto de los números complejos que encontramos en las ecuaciones de tres incógnitas.
Esta ecuación ha abierto el camino al desarrollo de la topología, una rama de las matemáticas modernas.
Y además de ayudarte a entender todas estas ecuaciones increíbles, las matemáticas te pueden servir para aumentar tu capacidad de seducción.
9. La transformada de Fourier
La transformada de Fourier divide el tiempo en varias frecuencias y ondas simples como un prisma desglosa la luz en varios colores.
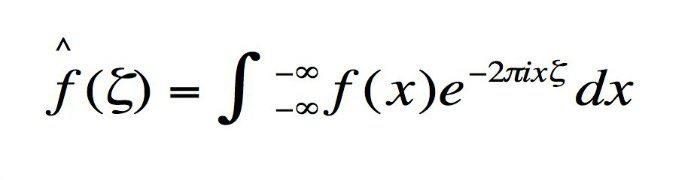
Otro ejemplo podría ser un campo magnético o un campo acústico, que se definen como una señal; la transformada de Fourier es su espectro: desestructura el campo acústico o magnético.
Esta teoría transformó nuestro mundo, ya que de repente era posible entender la estructura de las ondas más complejas como la del habla humana.
Actualmente, encontramos esta teoría, que data del 1822, en los procesamientos modernos de señal y de análisis, además de en el procesamiento de datos.
10. Las ecuaciones de Maxwell
Las ecuaciones de Maxwell describen cómo interactúan las cargas eléctricas y también las corrientes eléctricas y los campos magnéticos.
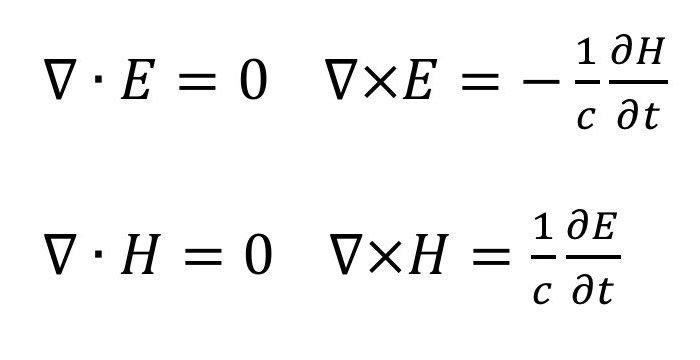
Explican el comportamiento de la relación entre la electricidad y el magnetismo. Son leyes esenciales y fundamentales de la física de hoy en día.
Hay cuatro formas de ecuaciones de Maxwell:
- Ecuación de Maxwell-Gauss
- Ecuación de Maxwell-Thomson
- Ecuación de Maxwell-Faraday
- Ecuación de Maxwell-Ampère
Debes saber que la música tiene ecuaciones escondidas. La transformada de Fourier, por ejemplo, permite descomponer un sonido complejo en notas simples, algo clave para los audífonos, el MP3 y hasta Spotify.
Si te interesa profundizar tus conocimientos, no dudes en acudir con un profesor de matematicas DF de Superprof y aprender todo lo que necesites.
11. El segundo principio de la termodinámica
El segundo principio de la termodinámica (también conocido como el principio de Carnot, que lo enuncia en 1824) prueba de manera irrefutable que los fenómenos físicos son irreversibles, principalmente cuando hay cambios térmicos.
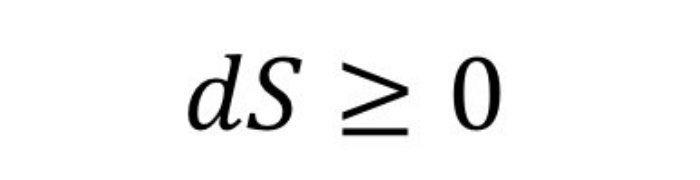
Este principio fue cambiado y reformulado en varias ocasiones y fue Ludwig Boltzmann en 1873 con Max Planck quienes lo popularizarán a gran escala.
Mientras que el primer principio de la termodinámica establece una equivalencia de diferentes formas de energía, como el calor y el trabajo (principio de conservación), el segundo principio introdujo otro sistema llamado entropía.
Es un principio de evolución, ya que determina en qué dirección las posibles transformaciones energéticas del mundo son factibles. Por lo tanto, se pueden dar ciertas transformaciones químicas, mientras que otras nunca lo se darán.
Por ejemplo, si pones un cubito de hielo en una taza de café caliente, verás que el cubito de hielo se derrite pero nunca verás que el café se congela.
Así, las mates tienen aplicaciones reales, si te gusta el póker, por ejemplo, descubre cómo las matemáticas te pueden ayudar a dominarlo.
12. La ecuación de Schrödinger
Si tuviéramos que ilustrar qué son las matemáticas y la mecánica cuántica, la ecuación de Schrödinger sería el ejemplo perfecto.
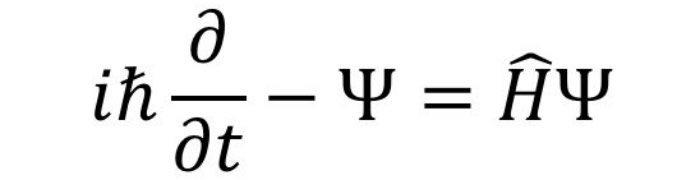
Al igual que la teoría de la relatividad general de Einstein pudo explicar el Universo a gran escala, esta ecuación arroja luz sobre el comportamiento de los átomos y las partículas subatómicas.
La ecuación de Schrödinger explica la evolución en el tiempo de una partícula. Describe los estados de esta partícula a partir de los cuales se puede describir todos los estados compuestos de partículas.
Esta ecuación plantea una auténtica cuestión filosófica, a saber: ¿la materia se compone de presencias de los estados posibles (gas, sólido, líquido)? ¿No hay nada más?
La aplicación de esta ecuación se encuentra en la tecnología moderna, como la energía nuclear, los ordenadores con semiconductores y los láseres.
Sin ecuaciones no habría exploración espacial, pues la ecuación de cohetes de Tsiolkovsky fue esencial para enviar satélites y astronautas al espacio.
13. Las ecuaciones de Navier Stokes
Encontramos estas ecuaciones en mecánica de fluidos. Describen el movimiento de fluidos newtonianos (gas y ciertos líquidos) que tienen la particularidad de tener derivadas parciales no lineares.
Aunque la coherencia matemática de estas ecuaciones (no lineares) no esté demostrada, a menudo permiten una modelización de fenómenos relativamente cercana de la realidad percibida.
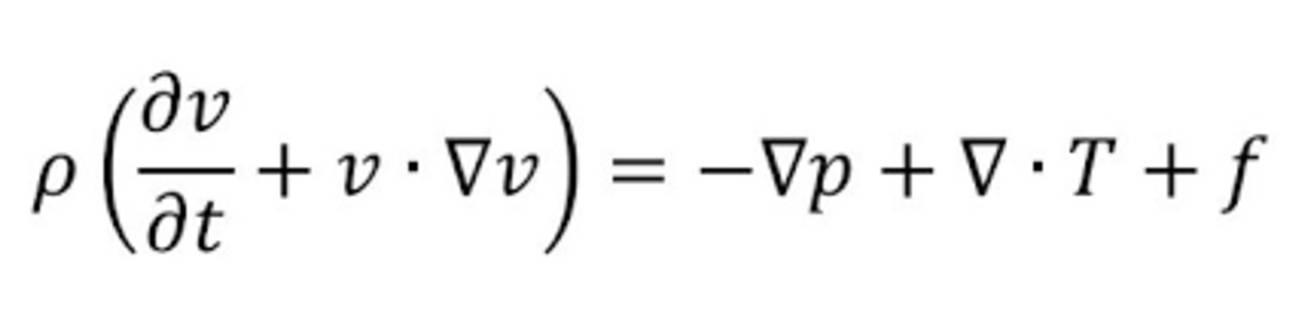
Estas ecuaciones son útiles en ámbitos como las corrientes oceánicas, la meteorología con los movimientos de masa de aire, el comportamiento de las construcciones (edificios, puentes) ante el impacto del viento o el comportamiento de los objetos lanzados a gran velocidad, como un tren o un avión frente al viento.
14. La teoría de la información de Shannon
Esta teoría haya sus fundamentos en el artículo A Mathematical Theory of Communication publicado en 1948 por Claude Shannon y será completada por Warren Weaber después. Esta teoría considera la información como una variable cuantificable, aunque no se pueda observar.
Una vulgarización de esta teoría consistiría en decir que se centra en cuantificar el contenido medio de información contenido en un mensaje o en un conjunto de mensajes.
Aunque la teoría de la información no se limita inicialmente más que al análisis de medios a poner en marcha para transmitir una información lo más eficazmente posible, muy pronto fue objeto de una reapropiación matemática, en especial a través de los trabajos del estadista Ronald Aylmer Fisher.
Fisher destaca el hecho de que una información es igual al valor medio del cuadrado de la derivada parcial (?) del logaritmo natural de la ley de probabilidad estudiada.
Es decir, cuanto más probable sea una información, menos información transmite y viceversa. El ejemplo de un presentador de telediario es representativo.
Algunas ecuaciones son consideradas tan bellas que se consideran arte matemático. De hecho, la Identidad de Euler ha sido llamada “la ecuación más hermosa del mundo” porque conecta cinco constantes fundamentales de forma sorprendente.
15. Las matemáticas para ganar la guerra: ¡el caso de la máquina Enigma!
Muchos ya habréis oído hablar de Enigma y su papel para descifrar mensajes alemanes durante la segunda guerra mundial.
Muchos historiadores están de acuerdo en que el critoanálisis de Enigma fue un factor mayor del éxito de los aliados y que indirectamente salvó muchas vidas y acortó la guerra.
El principio de base de la máquina Enigma se basa en 3 elementos que trabajan en cadena:
- El tablón de conexión que permite intercambiar de dos en dos las letras del alfabeto gracias a 6 "fichas" (se pueden por tanto cambiar de lugar 12 letras: la A se convierte por ejemplo en E y E se convierte en A, D puede seguir siendo D...),
- Los rotores que también cambian de lugar pero sin noción de reciprocidad, es decir, que si B se convierte en C, C no necesariamente se convierte en B. A medida que evoluciona la máquina Enigma, paseremos de 3 a 6 rotores. De esos 6 rotores, solo se utilizan tres para la codificación y se pueden colocar en cualquier orden. Aunque el rotor transforme inicialmente D en B, cuando sube un nivel, transforma C en A. El rotor comporta 26 niveles para igual número de posiciones. Después de 26 letras, vuelve a su posición inicial y es el segundo motor el que sigue. Así hasta el tercero,
- El reflector permite una última permutación. El objetivo es permutar de nuevo todas las letras de 2 en 2 que pasan después por los rotores y luego por la tabla de conexión.
La combinación de todas estas permutaciones hace aparecer 10^16 (10 elevado a 16) posibilidades de interpretación diferentes del código.

Si no has visto la película Imitation Game que trata el tema, ¡te la recomendamos! Y si deseas aprender más, toma cursos de matematicas en linea con un maestro de Superprof.
Superprof te lo resume
Las matemáticas están llenas de ecuaciones que han cambiado nuestra forma de entender el mundo, desde el teorema de Pitágoras hasta la famosa E = mc² de Einstein. Sin embargo, si hablamos de la ecuación más difícil del mundo, la respuesta no es tan simple: depende de a quién le preguntes.
Para un estudiante, una ecuación como 2x + 5 = 15 puede ser todo un reto. Sin embargo, en el terreno de las matemáticas avanzadas existen problemas tan complejos que ni siquiera los expertos han logrado resolverlos del todo.
Ejemplo de ello son las ecuaciones de Navier-Stokes, que describen cómo se mueven los fluidos. Aunque su fórmula parece sencilla, su resolución general es tan complicada que aún hoy sigue pendiente… y hasta existe un premio de un millón de dólares para quien logre resolverlas.
Lo mismo ocurre con la Ecuación de Yang–Mills, otro desafío abierto con recompensa millonaria.
En realidad, no hay “una única ecuación imposible”, sino un conjunto de problemas abiertos que llevan décadas, incluso siglos, desafiando a los matemáticos más brillantes.
Y lo fascinante es que resolverlos no es solo un ejercicio intelectual: también podría transformar áreas como la física, la ingeniería, la meteorología o la tecnología.
Resumir con IA:
















Cool
Exelente logre concluir las respuestas con promedio de 9.6 en 3hrs 45 min eso me deja en el 2do r lugar de todo el plantel